泊松分佈計算器
泊松分佈計算是用於描述在一個固定時間或空間內事件發生次數的機率分佈,常用於描述低機率事件的發生情況,如單位時間內某事件發生的次數。透過泊松分佈計算器,使用者可以線上快速計算得出泊松分佈的機率。這個工具提供了泊松分佈的機率公式以及相應的計算功能,旨在幫助使用者更好地理解和應用泊松分佈,提供便捷的泊松分佈計算功能。
| λ | |
|---|---|
| X (泊松隨機變數) | |
| 計算結果 | |
| 泊松分佈 | |
| 累積泊松分佈 | |
泊松分佈
泊松分佈是一種統計與機率學裡常見到的離散機率分佈,由法國數學家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年時發表。
機率論中常用的一種離散型機率分佈。若隨機變數 X 只取非負整數值,取k值的機率為
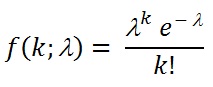
(k=0,1,2,…)
則隨機變數X 的分佈稱為泊松分佈,記作P(λ)。這個分佈是S.-D.泊松研究二項分佈的漸近公式是時提出來的。泊松分佈P (λ)中只有一個引數λ ,它既是泊松分佈的均值,也是泊松分佈的方差。在實際事例中,當一個隨機事件,例如某電話交換臺收到的呼叫、來到某公共汽車站的乘客、某放射性物質發射出的粒子、顯微鏡下某區域中的白血球等等,以固定的平均瞬時速率 λ(或稱密度)隨機且獨立地出現時,那麼這個事件在單位時間(面積或體積)內出現的次數或個數就近似地服從泊松分佈。因此泊松分佈在管理科學,運籌學以及自然科學的某些問題中都佔有重要的地位。